R-Squared Method in Forex Trading

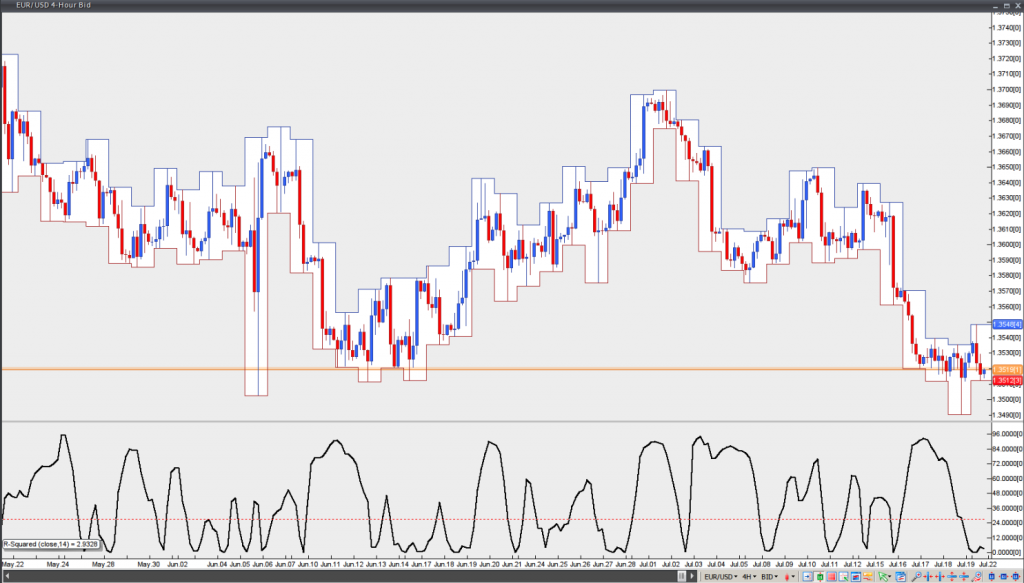
This is a linear regression method, which attempts to determine the strength of trends. If prices move in a straight line more closely during a certain period of time, this suggests that the trend will be stronger. R-Squared readings reflect the percentage of price movement in terms of linear regression. In case the R-Squared reading during 14 periods is at 60%, this indicates that 60% of the price move can be explained using linear regression. The remaining 40% is considered as random noise.

A trend is statistically significant for a linear regression line of a certain period, if we have a confidence level of 95%. In case the R-Squared reading is below the 95% confidence level for a particular period, then there is no statistically significant trend.

Below the recommended number of R-Squared periods and the corresponding 95% confidence levels are shown.

Number of Periods / R-Squared Critical Value equal to 95% Confidence:

5 / 77
10 / 40
14 / 27
20 / 20
25 / 16
30 / 13
50 / 8
60 / 6
120 / 3

Linear regression and R-Squared can be used in several ways in order to generate trading signals. One of the approaches combines the R-Squared with the Linear Regression Slope. The R-Squared will determine how strong the underlying trend is, while the Linear Regression Slope will determine the direction of the trend – whether it is positive or negative. Signals will be produced in accordance with the direction of the Linear Regression Slope, while the R-Squared should remain above its 95% level of confidence.

Another approach combines the R-Squared with an oscillator. In this case signals will be produced in accordance with the oscillators readings between the overbought and the oversold levels, while the R-Squared should remain at low levels (significantly below the 95% level of confidence, which suggests that markets behavior is ”less trendy”).

Chart Source: VT Trader